Matemática financeira - parte V

FLUXO DE CAIXA

    O fluxo de caixa serve para demonstrar graficamente as transações financeiras em um período de tempo. O tempo é representado na horizontal dividido pelo número de períodos relevantes para análise. As entradas ou recebimentos são representados por setas verticais apontadas para cima e as saídas ou pagamentos são representados por setas verticais apontadas para baixo. Observe o gráfico abaixo:

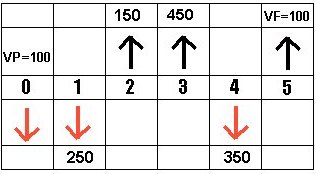
    Chamamos de VP o valor presente, que significa o valor que eu tenho na data 0; VF é ovalor futuro, que será igual ao valor que terei no final do fluxo, após juros, entradas e saídas. 

VALOR PRESENTE e VALOR FUTURO

    Na fórmula M = P . (1 + i)ⁿ , o principal P é também conhecido como Valor Presente (PV = present value) e o montante M é também conhecido como Valor Futuro (FV = future value). 

    Então essa fórmula pode ser escrita como 

    FV = PV (1 + i) ⁿ 

    Isolando PV na fórmula temos:

    PV = FV / (1+i)ⁿ

    Na HP-12C, o valor presente é representado pela tecla PV.

    Com esta mesma fórmula podemos calcular o valor futuro a partir do valor presente.

    Exemplo:

    Quanto teremos daqui a 12 meses se aplicarmos R$1.500,00 a 2% ao mês?
    Solução:

         FV = 1500 . (1 + 0,02)¹² = R$ 1.902,36

Matemática financeira - parte IV

Relação entre juros e progressões

    No regime de juros simples:
    M( n ) = P + n r P

    No regime de juros compostos:
    M( n ) = P . ( 1 + r ) ⁿ

    Portanto:

• num regime de capitalização a juros simples o saldo cresce em progressão aritmética
• num regime de capitalização a juros compostos o saldo cresce em progressão geométrica

TAXAS EQUIVALENTES

    Duas taxas i₁ e i₂ são equivalentes, se aplicadas ao mesmo Capital P durante o mesmo período de tempo, através de diferentes períodos de capitalização, produzem o mesmo montante final.

• Seja o capital P aplicado por um ano a uma taxa anual i_a .
• O montante M ao final do período de 1 ano será igual a M = P(1 + i _a )
• Consideremos agora, o mesmo capital P aplicado por 12 meses a uma taxa mensal i_m .
• O montante M’ ao final do período de 12 meses será igual a M’ = P(1 + i_m)¹² .

    Pela definição de taxas equivalentes vista acima, deveremos ter M = M’.

    Portanto, P(1 + i_a) = P(1 + i_m)¹²
    Daí concluímos que 1 + i_a = (1 + i_m)¹²
    Com esta fórmula podemos calcular a taxa anual equivalente a uma taxa mensal conhecida.

    Exemplos:

    1 - Qual a taxa anual equivalente a 8% ao semestre?

    Em um ano temos dois semestres, então teremos: 1 + i_a = (1 + i_s)²
    1 + i_a = 1,08²
    i_a = 0,1664 = 16,64% a.a.
   

    2 - Qual a taxa anual equivalente a 0,5% ao mês?

    1 + i_a = (1 + i_m)¹²
    1 + i_a = (1,005)¹²
    i_a = 0,0617 = 6,17% a.a.

TAXAS NOMINAIS

    A taxa nominal é quando o período de formação e incorporação dos juros ao Capital não coincide com aquele a que a taxa está referida. Alguns exemplos:
- 340% ao semestre com capitalização mensal.- 1150% ao ano com capitalização mensal.
- 300% ao ano com capitalização trimestral.

    Exemplo:

     Uma taxa de 15 % a.a., capitalização mensal, terá 16.08 % a.a. como taxa efetiva:

    15/12 = 1,25                    1,25¹² = 1,1608

TAXAS EFETIVAS

    A taxa Efetiva é quando o período de formação e incorporação dos juros ao Capital coincide com aquele a que a taxa está referida. Alguns exemplos:
- 140% ao mês com capitalização mensal.
- 250% ao semestre com capitalização semestral.
- 1250% ao ano com capitalização anual.

    Taxa Real: é a taxa efetiva corrigida pela taxa inflacionária do período da operação.

Matemática financeira - parte III

JUROS COMPOSTOS

    O regime de juros compostos é o mais comum no sistema financeiro e portanto, o mais útil para cálculos de problemas do dia-a-dia. Os juros gerados a cada período são incorporados ao principal para o cálculo dos juros do período seguinte.

    Chamamos de capitalização o momento em que os juros são incorporados ao principal.

Após três meses de capitalização, temos:

    1º mês: M =P.(1 + i)
    2º mês: o principal é igual ao montante do mês anterior: M = P x (1 + i) x (1 + i) 
    3º mês: o principal é igual ao montante do mês anterior: M = P x (1 + i) x (1 + i) x (1 + i)

    Simplificando, obtemos a fórmula:
  

M = P . (1 +  i)n

    Importante: a taxa i tem que ser expressa na mesma medida de tempo de n, ou seja, taxa de juros ao mês para n meses.

    Para calcularmos apenas os juros basta diminuir o principal do montante ao final do período:
  

J = M - P

    Exemplo:

   Calcule o montante de um capital de R$6.000,00, aplicado a juros compostos, durante 1 ano, à taxa de 3,5% ao mês.
  (use log 1,035=0,0149 e log 1,509=0,1788)

   Resolução:

   P = R$6.000,00
    t = 1 ano = 12 meses
    i = 3,5 % a.m. = 0,035
    M = ?

  

   Usando a fórmula M=P.(1+i)ⁿ, obtemos:

   M  =  6000.(1+0,035)¹²  =  6000. (1,035)¹²
    Fazendo  x = 1,035¹² e aplicando logaritmos, encontramos:

   log x = log 1,035¹²    =>   log x = 12 log 1,035    =>   log x = 0,1788    =>   x = 1,509

   Então  M = 6000.1,509 = 9054.

    Portanto o montante é R$9.054,00

Matemática financeira - parte II

JUROS SIMPLES

    O regime de juros será simples quando o percentual de juros incidir apenas sobre o valor principal. Sobre os juros gerados a cada período não incidirão novos juros. Valor Principal ou simplesmente principal é o valor inicial emprestado ou aplicado, antes de somarmos os juros. Transformando em fórmula temos:

J = P . i . n

Onde:

J = juros P = principal (capital) i = taxa de juros n = número de períodos

   

    Exemplo: Temos uma dívida de R$ 1000,00 que deve ser paga com juros de 8% a.m. pelo regime de juros simples e devemos pagá-la em 2 meses. Os juros que pagarei serão:

J = 1000 x 0.08 x 2 = 160

    Ao somarmos os juros ao valor principal temos o montante.

   Montante = Principal + Juros
   Montante = Principal + ( Principal x Taxa de juros x Número de períodos )

M = P . ( 1 + ( i . n ) )

    Exemplo: Calcule o montante resultante da aplicação de R$70.000,00 à taxa de 10,5% a.a. durante 145 dias.

    SOLUÇÃO:
    M = P . ( 1 + (i.n) )
    M = 70000 [1 + (10,5/100).(145/360)] = R$72.960,42

    Observe que expressamos a taxa i e o período n, na mesma unidade de tempo, ou seja, anos. Daí ter dividido 145 dias por 360, para obter o valor equivalente em anos, já que um ano comercial possui 360 dias.

---

   Exercícios sobre juros simples:

   1) Calcular os juros simples de R$ 1200,00 a 13 % a.t. por 4 meses e 15 dias.

    0.13 / 6 = 0.02167
    logo, 4m15d = 0.02167 x 9 = 0.195

    j = 1200 x 0.195 = 234

    2 - Calcular os juros simples produzidos por R$40.000,00, aplicados à taxa de 36% a.a., durante 125 dias.

    Temos: J = P.i.n
    A taxa de 36% a.a. equivale a 0,36/360 dias = 0,001 a.d.
    Agora, como a taxa e o período estão referidos à mesma unidade de tempo, ou seja, dias, poderemos calcular diretamente:
    J = 40000.0,001.125 = R$5000,00

    3 - Qual o capital que aplicado a juros simples de 1,2% a.m. rende R$3.500,00 de juros em 75 dias?

    Temos imediatamente: J = P.i.n ou seja: 3500 = P.(1,2/100).(75/30)
    Observe que expressamos a taxa i e o período n em relação à mesma unidade de tempo, ou seja, meses. Logo,
    3500 = P. 0,012 . 2,5 = P . 0,030; Daí, vem:
    P = 3500 / 0,030 = R$116.666,67

   4 - Se a taxa de uma aplicação é de 150% ao ano, quantos meses serão necessários para dobrar um capital aplicado através de capitalização simples?

   Objetivo: M = 2.P
    Dados: i = 150/100 = 1,5
    Fórmula: M = P (1 + i.n)
    Desenvolvimento:

2P = P (1 + 1,5 n)2 = 1 + 1,5 nn = 2/3 ano = 8 meses

Matemática Financeira

Conceitos básicos     A Matemática Financeira é uma ferramenta útil na análise de algumas alternativas de investimentos ou financiamentos de bens de consumo. Consiste em empregar procedimentos matemáticos para simplificar a operação financeira a um Fluxo de Caixa.     Capital O Capital é o valor aplicado através de alguma operação financeira. Também conhecido como: Principal, Valor Atual, Valor Presente ou Valor Aplicado. Em inglês usa-se Present Value (indicado pela tecla PV nas calculadoras financeiras).       Juros Juros representam a remuneração do Capital empregado em alguma atividade produtiva. Os juros podem ser capitalizados segundo dois regimes: simples ou compostos.        JUROS SIMPLES: o juro de cada intervalo de tempo sempre é calculado sobre o capital inicial emprestado ou aplicado. JUROS COMPOSTOS: o juro de cada intervalo de tempo é calculado a partir do saldo no início de correspondente intervalo. Ou seja: o juro de cada intervalo de tempo é incorporado ao capital inicial e passa a render juros também.        O juro é a remuneração pelo empréstimo do dinheiro. Ele existe porque a maioria das pessoas prefere o consumo imediato, e está disposta a pagar um preço por isto. Por outro lado, quem for capaz de esperar até possuir a quantia suficiente para adquirir seu desejo, e neste ínterim estiver disposta a emprestar esta quantia a alguém, menos paciente, deve ser recompensado por esta abstinência na proporção do tempo e risco, que a operação envolver. O tempo, o risco e a quantidade de dinheiro disponível no mercado para empréstimos definem qual deverá ser a remuneração, mais conhecida como taxa de juros.     Quando usamos juros simples e juros compostos?     A maioria das operações envolvendo dinheiro utiliza juros compostos. Estão incluídas: compras a médio e longo prazo, compras com cartão de crédito, empréstimos bancários, as aplicações financeiras usuais como Caderneta de Poupança e aplicações em fundos de renda fixa, etc. Raramente encontramos uso para o regime de juros simples: é o caso das operações de curtíssimo prazo, e do processo de desconto simples de duplicatas.     Taxa de juros     A taxa de juros indica qual remuneração será paga ao dinheiro emprestado, para um determinado período. Ela vem normalmente expressa da forma percentual, em seguida da especificação do período de tempo a que se refere: 8 % a.a. - (a.a. significa ao ano). 10 % a.t. - (a.t. significa ao trimestre).     Outra forma de apresentação da taxa de juros é a unitária, que é igual a taxa percentual dividida por 100, sem o símbolo %: 0,15 a.m. - (a.m. significa ao mês). 0,10 a.q. - (a.q. significa ao quadrimestre) Fonte: http://www.somatematica.com.br

TEORIA DOS CONJUNTOS

Símbolos

: pertence	: existe
: não pertence	: não existe
: está contido	: para todo (ou qualquer que seja)
: não está contido	: conjunto vazio
: contém	N: conjunto dos números naturais
: não contém	Z : conjunto dos números inteiros
/ : tal que	Q: conjunto dos números racionais
: implica que	Q'= I: conjunto dos números irracionais
: se, e somente se	R: conjunto dos números reais

Representações de Conjuntos

a) Extensão ou Enumeração

Quando o conjunto é representado por uma listagem ou enumeração de seus elementos. Devem ser escritos entre chaves e separados por vírgula ou ponto-e-vírgula.

Exemplos:

• Conjunto dos nomes de meus filhos: {Larissa, Júnior, Thiago, Juliana, Fabiana};
• Conjunto dos meses com menos de 31 dias: {fevereiro, abril, junho, setembro, novembro};
• Conjunto dos números pares inteiros maiores do que 8 e menores do que 22: {10; 12; 14; 16; 18; 20}.

Observações:

1. Na representação por extensão cada elemento deve ser escrito apenas uma vez;
2. É uma boa prática adotar a separação dos elementos em conjuntos numéricos como sendo o ponto-e-vírgula, para evitar confusões com as casas decimais: {2;3;4} e {2,3;4};
3. Esta representação pode, também, ser adotada para conjuntos infinitos em que se evidencia a lei de formação de seus elementos e colocando-se reticências no final: {2, 4, 6, 8, 10, …};
4. Representação semelhante pode ser adotada para conjuntos finitos com um grande número de elementos: {0, 1, 2, 3, …, 100}.

b) Propriedade dos Elementos

Representação em que o conjunto é descrito por uma propriedade característica comum a todos os seus elementos. Simbolicamente:

A = {x | x tem a Propriedade P}

e lê-se: A é o conjunto dos elementos x tal que (|) x tem a propriedade P.

Exemplos:

• A = {x | x é um time de futebol do Campeonato Brasileiro de 2006};
• B = {x | x é um número inteiro par e 8 < x < 22}. Último exemplo do item a) acima;
• C = {x | x é um deputado federal eleito em 2006}.

c) Diagrama de Euler-Venn

Um conjunto pode ser representado por meio de uma linha fechada e não entrelaçada, como mostrado na figura abaixo. Os pontos dentro da linha fechada indicam os elementos do conjunto.

Conjunto Unitário e Conjunto Vazio

Embora o conceito intuitivo de conjunto nos remeta à idéia de pluralidade (coleção de objetos), devemos considerar a existência de conjunto com apenas um elemento, chamados de conjuntos unitários, e o conjunto sem qualquer elemento, chamado de conjunto vazio (Ø).

O conjunto vazio é obtido quando descrevemos um conjunto onde a propriedade P é logicamente falsa.

Exemplos de Conjuntos Unitários:

• Conjunto dos meses do ano com menos de 30 dias: {fevereiro};
• Conjunto dos números inteiros maiores do que 10 e menores do que 12: {11};
• Conjunto das vogais da palavra blog: {o}.

Exemplos de Conjuntos Vazios:

• {x | x > 0 e x < 0} = Ø;
• Conjunto dos meses com mais de 31 dias;
• {x | x² = -1 e x é um número real} = Ø.

Conjunto Universo

É o conjunto ao qual pertencem todos os elementos envolvidos em um determinado assunto ou estudo, e é simbolizado pela letra U.

Assim, se procuramos determinar as soluções reais de uma equação do segundo grau, nosso conjunto Universo U é R (conjunto dos números reais); se estamos interessados em determinar os deputados federais envolvidos com o mensalão, nesse caso o universo U tem como elementos todos os deputados federais da atual legislatura.

Portanto, é essencial, que ao descrever um conjunto através de uma propriedade P, fixemos o conjunto universo em que estamos trabalhando, escrevendo:

Igualdade de Conjuntos

Dois conjuntos A e B são iguais quando todo elemento de A pertence a B e, reciprocamente, todo elemento de B pertence a A:

Observações:

1. A título de ilustração: O A invertido na expressão acima significa “para todo”;
2. {a, b, c, d} = {d, b, a, c}. O que demonstra que a noção de ordem não interfere na igualdade de conjuntos;
3. É evidente que para A ser diferente de B é suficiente que um elemento de A não pertença a B ou vice-versa: A = {a, b, c} é diferente de B = {a, b, c, d}.

Subconjunto

Um conjunto A é um subconjunto de (está contido em) B se, e sómente se, todo elemento x pertencente a A também pertence a B:

onde a notaçãosignifica “A é subconjunto de B” ou “A está contido em B” ou “A é parte de B”. A leitura da notação no sentido inverso é feita como “B contém A”. Observe que a abertura do sinal de inclusão fica sempre direcionado para o conjunto “maior”. Na forma de diagrama é representado como:

Exemplos:

• {1; 2; 3} C {1; 2; 3; 4; 5; 6}
• Ø C {a, b};
• {a, b} C {a, b};
• {a, b, c} ¢ {a, c, d, e}, onde ¢ significa “não está contido”, uma vez que o elemento b do primeiro conjunto não pertence ao segundo.

Observe que na definição de igualdade de conjuntos está explícito que todo elemento de A é elemento de B e vice-versa, ou seja, que A está contido em B e B está contido em A. Assim, para provarmos que dois conjuntos são iguais devemos provar que:

Propriedades da Inclusão

Sejam D, E e F três conjuntos quaisquer. Então valem as seguintes propriedades:

1. Ø C D: O conjunto vazio é subconjunto de qualquer conjunto;
2. D C D: Todo conjunto é subconjunto de si próprio (propriedade Reflexiva);
3. D C E e E C D => D = E: veja acima (propriedade Anti-Simétrica);
4. D C E e E C F => D C F: Se um conjunto é subconjunto de um outro e este é subconjunto de um terceiro, então o primeiro é subconjunto do terceiro (propriedade Transitiva).

Com exceção da primeira propriedade, a demonstração das demais é bastante intuitiva e imediata. Vamos, portanto, provar a primeira:

Partimos da tese de que se o conjunto vazio não é um subconjunto de D, então é necessário que pelo menos um elemento desse conjunto não esteja contido no conjunto D. Como o conjunto vazio não possui nenhum elemento, a sentença Ø ¢ D é sempre falsa. Logo, o conjunto vazio está contido em D é sempre verdadeira.

Conjunto das Partes

Chama-se Conjunto das Partes de um conjunto E – P(E) – o conjunto formado por todos os subconjuntos de E:

Exemplos:

• Se A = {a, b, c}, então P(A) = {Ø, {a}, {b}, {c}. {a.b}, {a.c}. {b,c}, {a,b,c}}
• Se B = {a, b}, então P(B) = {Ø, {a}, {b}, {a,b}};
• Se C = {a}, então P(C) = {Ø, {a}}.

Observações:

1. Enfatizo, apesar de colocado na própria definição, que os elementos de P(E) são conjuntos;
2. Assim, deve-se ter atenção quanto ao emprego dos símbolos pertence (não pertence) e contido (não contido);
3. No primeiro exemplo acima: {a} pertence a P(A) e {{a}} é um subconjunto de P(A);
4. Se definirmos n(E) como sendo o número de elementos do conjunto E, então n(P(E)) = 2^n(E). A propriedade é válida para conjuntos finitos;
5. Veja nos exemplos: n(A) = 3 e n(P(A)) = 8 = 2³, n(B) = 2 e n(P(B)) = 4 = 2² e n(C) = 1 e n(P(C)) = 2 = 2¹.

A demonstração do item 5. é feita pelo Princípio da Indução Finita e será feita oportunamente.

Por enquanto é só. Aguardem o próximo artigo. Enquanto isto dê a sua opinião nos comentários, ela é muito importante.

Diagrama deVenn

Através de estudos relacionados à lógica, Jon Venn criou uma diagramação baseada em figuras no plano, esse método consiste basicamente em círculos que possuem a propriedade de representar relações entre conjuntos numéricos. Também pode ser utilizado no estudo da Estatística, a fim de organizar e analisar dados colhidos em pesquisas de opinião. Geralmente usamos os seguintes modelos de diagramas: 

Representação de conjunto único Números Naturais (1, 2, 3, 4, 5, 6) 

Relação entre dois conjuntos: A e B. A = (1, 2, 3, 4, 5, 6) 
B = (5, 6, 7, 8, 9, 10) 

Símbolos 
U = união 
∩ = intersecção 

A U B = (1, 2, 3, 4, 5, 6, 7, 8, 9, 10) 
A ∩ B = (5, 6) 

Relação entre três conjuntos: A, B e C. 
A = (3, 4, 5, 6, 7, 8) 
B = (4, 6, 8, 10, 12) 
C = (1, 2, 3, 4, 6, 10) 


A U B = (3, 4, 5, 6, 7, 8, 10, 12) 
A U C = (1, 2, 3, 4, 5, 6, 7, 8, 10) 
B U C = (1, 2, 3, 4, 6, 8, 10, 12) 
A ∩ B = (4, 6, 8) 
A ∩ C = (3, 4, 6) 
C ∩ B = (4, 6, 10)

Podemos observar através dos exemplos que os diagramas representam de uma forma prática eeficiente as relações de união e de intersecção entre os conjuntos numéricos. Eles podem ser usados na representação de quaisquer conjuntos, no intuito de estabelecer uma melhor demonstração e compreensão dos elementos pertencentes ao conjunto